Trees
Some layout algorithms require your graph to be a tree and we explain in some details in this page the various concepts related to trees.
In a somewhat mathematical lingo one would define a tree a connected graph without undirected cyclic edge paths. That is, a tree is a special type of graph with the following characteristics: - It is connected, meaning there is a path between any two nodes. - It has no cycles (also known as loops), which means there are no closed paths where you can start at one node and return to it by following edges. - It is acyclic, ensuring that there are no repeated edges or loops. - It has a unique root node from which all other nodes descend. - Each node (except the root) has exactly one parent node. - Nodes can have zero or more child nodes.
Visually, you can think of a tree as something like this (check this playground):
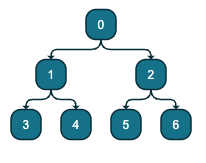
but as soon as you add anywhere an edge this breaks the tree structure:
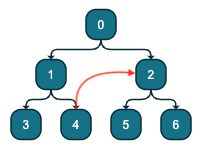
(check the playground )
In a tree, one speaks of a Leaf Node (or External Node) if the node has the following properties:
- a leaf node is a fundamental component of a tree.
- a leaf node is a node that does not have any child nodes.
- in simpler terms, it’s a node with no offspring.
- leaf nodes are also referred to as terminal nodes.
- these nodes mark the endpoints of a tree’s branches.
- unlike other nodes, leaf nodes do not branch out further.
- they represent the bottommost level of the tree.
- in mathematical terms, a leaf node has a degree of 0 (no children).
Sometimes one also refers to a leaf node if the graph is not a tree. In this case, it means a node with a single edge pointing towards it.
An ancestor or parent Node is defined as any node on the path from the root to a leaf node is called an ancestor of that leaf node.
The height of a Tree:
- The height of a tree is the maximum number of levels from the root to any leaf node.
- It represents the longest downward path within the tree.
- The height of the root node itself is 1.
- The height of the entire tree is the height of its root.
A tree level or depth is defined as follows:
- The root node (the topmost node) is considered level 0.
- Its immediate children are at level 1.
- Their children (and so on) are at subsequent levels (e.g., level 2, level 3, and so forth).
In summary, levels in a tree graph help organize nodes based on their distance from the root, providing a clear hierarchy
A forest is in essence a collection of trees:
- it consists of a collection of trees, where each tree is a separate component.
- unlike a single tree, a forest does not need to be connected (i.e., it can have multiple disjoint parts).
- there are no cycles (loops) within a forest
Trees are everywhere and the predictable (topological) structure of nodes in a tree make them ideal in all sorts of situations:
Hierarchical Structure:
- a tree exhibit a natural hierarchy, making them ideal for representing relationships between objects or concepts.
- the root node serves as the highest level, and child nodes branch out from it.
- examples include family trees, organizational hierarchies, and file systems.
Efficient Searching:
- binary search trees (a specific type of tree) allow efficient searching, insertion, and deletion operations.
- the logarithmic height of balanced trees ensures quick access to data.
Sorting and Traversal:
- Ii-order, pre-order, and post-order traversals allow systematic exploration of tree nodes.
- these traversals are essential for sorting algorithms and expression evaluation.
Binary Trees:
- binary trees have at most two children per node.
- they are used for efficient data storage (e.g., binary search trees, heaps).
Balanced Trees:
- balanced trees maintain a roughly equal height for subtrees.
- examples include AVL trees and red-black trees.
- balancing ensures efficient operations and prevents worst-case scenarios.
Decision Trees:
- decision trees help make decisions based on input features.
- commonly used in machine learning for classification and regression tasks.
Spanning Trees:
- spanning trees cover all nodes of a connected graph without forming cycles.
- minimum spanning trees minimize edge weights (e.g., Kruskal’s or Prim’s algorithms).
Expression Trees:
- expression trees represent mathematical expressions.
- useful for evaluating expressions and optimizing computations.
Parse Trees:
- parse trees represent the syntactic structure of sentences in natural language processing.
- they break down sentences into phrases and grammatical components.
Tree Traversal Algorithms:
- depth-first search (DFS) and breadth-first search (BFS) explore tree nodes efficiently.
- DFS includes in-order, pre-order, and post-order traversals.
- BFS visits nodes level by level.
Tree Height and Depth:
- the height of a tree is the longest path from the root to a leaf node.
- depth refers to the level of a specific node.
- these metrics impact efficiency and memory usage.
Tree Pruning:
- pruning removes unnecessary branches from a tree.
- common in decision trees and search algorithms.