Quantum Computing Intro

Quantum
An overview of these notes on (topological) quantum computing.

In this introduction on topological quantum computing (TQC) I want to give you a broad conceptual overview of how various fields come together. Specifically, how the following topics converge into TQC and form the foundation of quantum computing:

First, why would one wish to study all of this? It depends. If your daily duty is to boast line-of-business apps it’s not a subject you will benefit from. The same can be said, however, about studying general relativity or Darwinian evolution. Still, we all use cell phones and GPS which rely on general relativity for precise positioning. We all use Amazon’s store which relies on genetic algorithms for delivery optimization. Similarly, understanding (topological) quantum computing is not so much about giving you a direct benefit as it is about a broad framework underpinning the future of computing. The momentum towards abstraction (and the usage of mathematics) parallels our (technological) growth. Topological quantum computing is an awe inspiring subject bringing together rich ideas and beautiful maths. The (software) industry will eventually cover all of this with meta-frameworks (think Microsoft Q#) and hide all the gory details but understanding it gives you a broader appreciation. Climbing a mountain brings unexpected joys and satisfaction the casual mountain-lift tourist does not gain.

Second, what is the executive summary here? Topological quantum computing is about a particular implementation of quantum computers less prone to errors due to influences from outside the system, i.e. noise and instability. Think of a knotted bundle of wires. Throw it in the air, shake it, stretch it. It does not unknot. The information contained in the knotted structure is noise resistant. You can think of a quantum algorithm as a bundle of knots. The mathematical description of this demands quantum field theory and the topics enumerated above.

Next, let’s review a bit the basics.

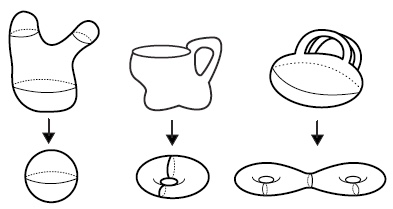
What is topology? It’s the study of how (open) sets describe objects (think of a surface or a tea cup). It describes how a sphere differs from a torus, how knot differs from a not-knot (unknot). Topology does not differentiate a sphere and an ellipsoid, differential geometry does. So, when one speaks of a topological property it means that it’s invariant under deformations (technically: diffeomorphisms). The knotted structure is a topological property, the hole in a donut is one as well.

The hole in the donut does not disappear by stretching it (breaking is not allowed, it’s not a smooth deformation). A quantum algorithm in the shape of a braid is topological (as illustrated below; the arrows indicate exchanges).

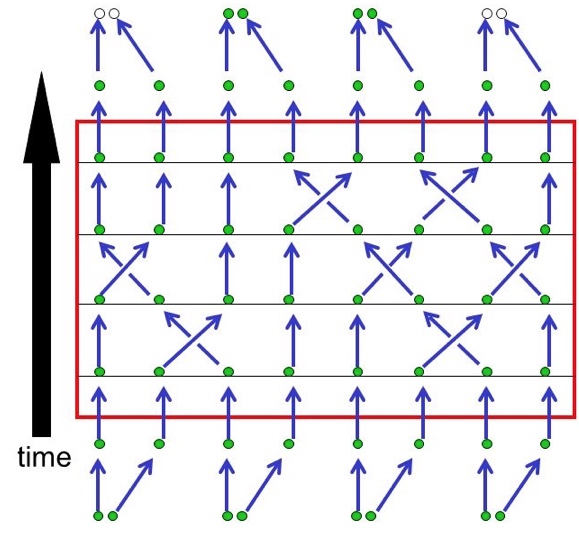
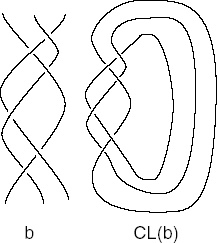
What are knots and braids? The idea that a knot can be unknotted through shuffling and shifting can be made mathematically precise and corresponds to maps of knots to numbers and polynomials. Braids and knots are one and the same thing and there is a famous theorem proving that you can look at a braid as a knot and vice versa. The idea is illustrated below. Braids are sometimes easier to use because there is a sense of direction you don’t have with knots. If you think of ‘time’ as a vertical axis in the image below you can imagine that the braid represents a interaction between particles. The interaction in the braid can be described through group theory and group representations. It’s a 2D representation of things. The knot-picture, on the other hand, is a 3D thing and allows other techniques (e.g. path integrals).

What is (general) relativity? Relativity deals with observers and how they can communicate their findings. If they have a steady speed you need special relativity, if they accelarate you need general relativity. The general theory embraces gravitation and is related to ‘curvature’. The concept of curvature is really the common idea of something bending and if you look at a knot you can immediately recognize that the amount of curvature is related to how knotted it is. At the same time, one needs relativity because things at a subatomic level happen very fast. Lightning speed-of-light fast. In order to account for the difference between our human pace and the subatomic one you need relativity. Technically speaking, relativity introduces the concept of a metric. A metric measures things. If you would walk on a donut you would walk a certain distance. If you would stretch the donut you would walk a different distance. Now, here is the crucial bit; certain things critically depend on a metric and some don’t. The latter are called topological because they do not depend on the precise shape but only on the global appearance. The number of holes does not depends on distances. So, you have a clash if you wish; on the one hand you need relativity to account for the speedy things and on the other hand you want to describe things as if they only depend on the global topology. This is the subject of topological quantum field theory.

What are anyons? Our universe consists of two families of particles, they are called bosons and fermions. Think +1 and -1. Describing them differs significantly though everything is beautifully unified in the so-called standard model. It’s a mixture of commuting and anti-commuting variables (remember, numbers commute while matrices don’t). The statistics of the particles is related to the concept of how identical things can be exchanged and that if you have a quantity based on identical things the exchange should not alter the quantity. Imagine a box filled with identical marbles and a number based on these marbles. An exact exchange of two marbles should not influence the number. This is called a symmetry and describing symmetries is the essence of group theory. These symmetries are intimately related to the dimensions of space and if we speak of two families it’s because we intrinsically assume that space is three-dimensional. At this point, you can look up things about strings and supersymmetry and discover that you can invent very different universes if you embrace higher dimensions. At the same time, if you look at 2D rather than 3D you also discover that things can be very different. Rather than having two families you have an infinite amount of families. Or rather, instead of having +1 or -1 you can have everything in between. Instead of bos-ons and fermi-ons you have any-ons. Anyons are however not ‘real’, they are pseudo-particle or quasi-particles (quarticles). Anyons are like waves on a river; the wave is created on top of water molecules while not itself a molecule. Physics is full of quarticles via the particle-wave duality; phonons, solitons, magnons, plasmons, rotons, skyrmions and whatnot.

What is quantum field theory (QFT)? Broadly speaking, quantum mechanics describes single non-interacting particles moving slowly. QFT describes arbitrary processes; many particles, speed of light stuff, things appearing and disappearing (particle creation and annihilation), things moving backwards in time and more. Describing your microwave in the kitchen demands QFT. Quantum mechanics (QM) is a simplified view of the world. The only electron of an hydrogen atom can be described with QM but does not accept interactions with light (photons). QFT requires you to master a whole lot of (mathematical) techniques going far beyond the things used in standard quantum computing (basically qubit and gates). There isn’t an easy way really and if you want to also grasp general relativity you are in for a some years of study. From a software point of view the subject is linked to operator product expansions (OPE), lattice theory and discrete simulation, discrete differential geometry (particle clouds and so on), asymptotic expansion and numerical solutions of integrals. SymPy and Mathematica support a small subset of QFT and the real big efforts are (based on C) proprietary frameworks.

What is Chern-Simons theory? It’s a TQFT tightly linked to how one can describe knots and their braids (interactions). It’s the bridge between the quantum world and topology. It’s one of those playgrounds where math meets physics in a deep passionate dance which inevitably involves intricate techniques (see e.g. Floer cohomology and Donaldson theory). For now, you can think of it as how anyons interact and how to turn braids into computations.

With all of this in place let’s move on to the crux of the matter. How does all of this hang together? Quantum computing is about using the AND-like superposition of states instead of the OR-like states of classical bits. Classical computing is deterministic while quantum computing is probabilistic. A quantum algorithm consists in using unitary transformations to transition one state into another. The term ‘unitary’ has a precise technical meaning but conceptually it amounts to saying that probability needs to be conserved (in the absence of external interactions). A unitary operator is however an abstract operator which can have many guises, known as representations. The representation hangs together (when looking at concrete physical systems) with the type of stuff you work with; laser light, hydrogen atoms, electron spin, magnetic force and so on. Quantum computing tells you how to compute things but does not tell you how to physically implement things. Indeed, one can play with QM and QFT for a long time without even thinking of real-world phenomena. As such, there are various ways to articulate quantum computers and how unitary evolution happens. One of the possible paths is based on anyons. As explained before, anyon interactions can be viewed as braids created in 2+1 dimensions. An anyon lives in 2D and is a particular type of quantum field. Being just another QFT it comes with all the machinery of operators, path integrals and whatnot. At the same time, it’s somewhat different because the interactions do not depends on precise positions in space and time but only on global topological properties. It only depends in how knotted the whole process is. So, you can look at a quantum computation based on anyons in different ways: as a braid (and the whole theory of knots with it), as a quantum field theory (with a century of tools and techniques), as the realization of a quantum algorithm. This trinity is what makes topological quantum computing a fertile playground and an interesting way to architect hardware.