from ortools.sat.python import cp_model
import matplotlib.pyplot as plt
import matplotlib as mpl
class MaintenanceScheduleSolver:
def __init__(self, rooms, personnel, availability, skills, times, delays, lunch_break, lunch_duration):
"""
Initializes the scheduling model with the given parameters.
Args:
rooms (list): List of rooms to be maintained.
personnel (list): List of personnel available for maintenance.
availability (dict): Dictionary mapping personnel to their availability times.
skills (dict): Dictionary mapping personnel to their skill sets.
times (dict): Dictionary mapping rooms to the time required for maintenance.
delays (dict): Dictionary mapping personnel to the delay times between rooms.
lunch_break (int): Fixed start time for the lunch break.
lunch_duration (int): Fixed duration of the lunch break.
Attributes:
rooms (list): List of rooms to be maintained.
personnel (list): List of personnel available for maintenance.
availability (dict): Dictionary mapping personnel to their availability times.
skills (dict): Dictionary mapping personnel to their skill sets.
times (dict): Dictionary mapping rooms to the time required for maintenance.
delays (dict): Dictionary mapping personnel to the delay times between rooms.
lunch_break (int): Fixed start time for the lunch break.
lunch_duration (int): Fixed duration of the lunch break.
num_rooms (int): Number of rooms to be maintained.
num_personnel (int): Number of personnel available for maintenance.
model (cp_model.CpModel): The constraint programming model.
assignments (dict): Dictionary to store room assignments for personnel.
start_times (dict): Dictionary to store start times for room maintenance.
end_times (dict): Dictionary to store end times for room maintenance.
before_lunch_constraints (dict): Constraints for tasks before lunch break.
after_lunch_constraints (dict): Constraints for tasks after lunch break.
"""
self.rooms = rooms
self.personnel = personnel
self.availability = availability
self.skills = skills
self.times = times # Time required to maintain each room
self.delays = delays # Delay between rooms for each personnel
self.lunch_break = lunch_break # Fixed lunch break start time
self.lunch_duration = lunch_duration # Fixed lunch break duration
self.num_rooms = len(rooms)
self.num_personnel = len(personnel)
self.model = cp_model.CpModel()
self.assignments = {}
self.start_times = {}
self.end_times = {}
self.before_lunch_constraints = {}
self.after_lunch_constraints = {}
self.create_variables()
self.add_constraints()
def create_variables(self):
"""
Creates decision variables for the assignment of personnel to rooms and start times.
"""
# Flatten the 2D list self.delays
flattened_delays = [delay for sublist in self.delays for delay in sublist]
# Calculate the upper bound for the start and end times
upper_bound = sum(self.times) + sum(flattened_delays)
for r in range(self.num_rooms):
for p in range(self.num_personnel):
# Assignment variable: 1 if person p is assigned to room r, else 0
self.assignments[(r, p)] = self.model.NewBoolVar(f'assign_r{r}_p{p}')
# Start time variable for each room and personnel
self.start_times[(r, p)] = self.model.NewIntVar(0, upper_bound, f'start_r{r}_p{p}')
# End time is derived from start time and the room's maintenance duration
self.end_times[(r, p)] = self.model.NewIntVar(0, upper_bound, f'end_r{r}_p{p}')
self.before_lunch_constraints[(r, p)] = self.model.NewBoolVar(f'before_lunch_r{r}_p{p}')
self.after_lunch_constraints[(r, p)] = self.model.NewBoolVar(f'after_lunch_r{r}_p{p}')
def add_constraints(self):
"""Adds constraints to the model."""
# Ensure each room is assigned exactly to one available and skilled person
for r in range(self.num_rooms):
room_type = self.rooms[r]
self.model.AddExactlyOne(self.assignments[(r, p)] for p in range(self.num_personnel) if self.skills[p][room_type])
# Ensure that the maintenance person respects the skill requirement and availability
for p in range(self.num_personnel):
# total_rooms_assigned = sum(self.assignments[(r, p)] for r in range(self.num_rooms))
# self.model.Add(total_rooms_assigned <= self.availability[p])
total_time = sum(self.times[r] * self.assignments[r, p] for r in range(self.num_rooms))
self.model.Add(total_time <= self.availability[p])
person_intervals = []
# Add time constraints: the start time, end time, and delays between consecutive tasks
for r in range(self.num_rooms):
if self.skills[p][self.rooms[r]]:
room_duration = self.times[r]
room_delay = self.delays[p][r]
# End time = Start time + Duration of the room + Delay between rooms
self.model.Add(self.end_times[(r, p)] == self.start_times[(r, p)] + room_duration + room_delay).OnlyEnforceIf(self.assignments[(r, p)])
interval = self.model.NewIntervalVar(self.start_times[(r, p)], room_duration + room_delay, self.end_times[(r, p)], f"interval_r{r}_p{p}")
person_intervals.append(interval)
# ensure intervals do not overlap
self.model.AddNoOverlap(person_intervals)
# Add lunch break constraint: no maintenance during lunch
for r in range(self.num_rooms):
room_duration = self.times[r]
# Lunch break (start times must not conflict with lunch time)
self.model.Add(self.start_times[(r, p)] + room_duration <= self.lunch_break).OnlyEnforceIf(self.before_lunch_constraints[(r, p)])
self.model.Add(self.start_times[(r, p)] + room_duration > self.lunch_break).OnlyEnforceIf(self.before_lunch_constraints[(r, p)].Not())
self.model.Add(self.start_times[(r, p)] >= self.lunch_break + self.lunch_duration).OnlyEnforceIf(self.after_lunch_constraints[(r, p)])
self.model.Add(self.start_times[(r, p)] < self.lunch_break + self.lunch_duration).OnlyEnforceIf(self.after_lunch_constraints[(r, p)].Not())
self.model.AddBoolOr(
[
self.before_lunch_constraints[(r, p)],
self.after_lunch_constraints[(r, p)]
]
)
def visualize_gantt_chart(self, solver):
fig, ax = plt.subplots(1, 1, figsize=(12, 5 + self.num_personnel / 8))
ax.set_xlabel('Time')
ax.set_ylabel('Personnel')
bar_style = {'alpha': 1.0, 'lw': 25, 'solid_capstyle': 'butt'}
text_style = {'color': 'white', 'weight': 'bold', 'ha': 'center', 'va': 'center', 'fontsize': 8}
colors = mpl.cm.Dark2.colors
ax.set_yticks([10 * i for i in range(self.num_personnel)])
ax.set_yticklabels([f'Person {i}' for i in range(self.num_personnel)])
# Draw a band for the lunch break
ax.axvspan(self.lunch_break, self.lunch_break + self.lunch_duration, facecolor='orange', alpha=0.5)
ax.text(self.lunch_break + self.lunch_duration / 2, self.num_personnel / 2 + 5, 'Lunch Break', rotation=90, va='center', ha='center', color='black', fontsize=12, alpha=0.7)
for p in range(self.num_personnel):
for r in range(self.num_rooms):
if solver.BooleanValue(self.assignments[(r, p)]):
start_time = solver.Value(self.start_times[(r, p)])
end_time = solver.Value(self.end_times[(r, p)])
ax.broken_barh([(start_time, end_time - start_time)], (10 * p - 5, 9), facecolors=('tab:blue'), edgecolor='white')
ax.text(start_time + (end_time - start_time) / 2, 10 * p, f'Room {r} [{self.times[r]}]', **text_style)
# fig.tight_layout()
plt.show()
def schedule_for_person(self, p):
"""
Returns the schedule for a given person.
The schedule is a list of tuples (start_time, end_time, room, duration).
"""
schedule = []
for r in range(self.num_rooms):
if solver.BooleanValue(self.assignments[(r, p)]):
start_time = solver.Value(self.start_times[(r, p)])
end_time = solver.Value(self.end_times[(r, p)])
schedule.append((start_time, end_time, r, end_time - start_time))
schedule.sort(key=lambda x: x[0])
return schedule
def solve(self):
"""Solves the scheduling problem and prints the result."""
solver = cp_model.CpSolver()
status = solver.Solve(self.model)
if status == cp_model.OPTIMAL or status == cp_model.FEASIBLE:
print('Solution:')
self.visualize_gantt_chart(solver)
for p in range(self.num_personnel):
print(f'Person {p}:')
schedule = []
for r in range(self.num_rooms):
if solver.BooleanValue(self.assignments[(r, p)]):
start_time = solver.Value(self.start_times[(r, p)])
end_time = solver.Value(self.end_times[(r, p)])
schedule.append((start_time, end_time, r))
schedule.sort(key=lambda x: x[0])
for start_time, end_time, r in schedule:
print(f' [{start_time}, {end_time}]: {r}')
else:
print('No solution found.')Scheduling using Google OR Tools
The use-case is similar to the job shop problem (JSP) and is as follows:
- there are locations which have to be serviced by a team of workers. Each location has a type and a duration
- there are workers who have different skills and can work on different types of locations
- between servicing a location there is a variable delay
- the schedule has to respect lunch breaks and the maximum working hours of the workers
- the objective function is to minimize the total time to service all locations.
📘 The book entitled “A book on open shop scheduling” by Wieslaw Kubiak provides a good introduction to the topic.
🐺 You can also find a simplified approach using Wolfram on Orbifold’s Journal.
🧑💻 The code can be found on GitHub
Setup
The Google OR Tools library is open source, easy to use and the documentation is fairly complete. You can install it using the following command:
!pip install ortools matplpotlibIn comparison with high-end tools like Gurobi or Hexaly, OR Tools is more limited in terms of the number of variables and constraints it can handle. However, it is free and open source, and it is more than enough for many practical problems.
Variables
Like any other constraint optimization, the recipe is as follows:
- define the variables holding the information to optimize
- define the constraints that these variables have to satisfy
- define the objective function to minimize or maximize
- run the solver.
In this case, the variables are the following:
- start_times: the time at which a worker starts servicing a location
- end_times: the time at which a worker finishes servicing a location
- delays: the time between servicing two locations
- lunch_break: the time at which a worker takes a break
- lunch_duration: the duration of the break
- rooms: the location to be serviced
- personnel: the worker servicing the location
- availability: the time at which a worker is available
- skills: the skills of the workers
- delays: the time between servicing two locations
- times: the time to service a location.
Constraints
The constraints are the following:
- start_times and end_times are related by the duration of the location
- delays are related to the end_times of the previous location
- lunch_break is related to the start_times and end_times of the locations
- availability is related to the start_times and end_times of the locations
- skills are related to the rooms.
Objective function
The objective function is to minimize the total time to service all locations.
Solver
Creating the variables is the easy part. The constraints is where you need to fiddle a bit with how the API works. Things like OnlyEnforceIf and OnlyEnforceIf are not always intuitive.
Example
Let’s consider a handful of people and locations. The locations have a type and a duration. The people have skills and availability. The goal is to minimize the total time to service all locations:
# Example data
rooms = ['type_A', 'type_B', 'type_C', 'type_B', 'type_A', 'type_B', 'type_C', 'type_C'] # Room types (4 rooms)
personnel = ['P0', 'P1', 'P2', 'P3', 'P4'] # Personnel (5 people)
# Availability: Maximum number of rooms each person can handle
availability = [10, 3, 15, 10, 8]
# Skills: Which rooms each person can maintain
skills = [
{'type_A': True, 'type_B': False, 'type_C': True}, # P1
{'type_A': True, 'type_B': True, 'type_C': False}, # P2
{'type_A': False, 'type_B': True, 'type_C': True}, # P3
{'type_A': False, 'type_B': True, 'type_C': True}, # P4
{'type_A': False, 'type_B': False, 'type_C': True}, # P5
]
# Time required for each room (in arbitrary time units)
times = [6, 4, 2, 3, 2, 4, 2, 3]
# Delays between rooms for each personnel (in arbitrary time units)
delays = [
[0, 1, 2, 1, 0, 1, 2, 1], # Delays for P0 between rooms
[1, 0, 1, 2, 0, 1, 0, 1], # Delays for P1 between rooms
[0, 1, 0, 1, 0, 1, 0, 1], # Delays for P2 between rooms
[0, 1, 0, 1, 0, 1, 0, 1], # Delays for P3 between rooms
[0, 1, 0, 1, 0, 1, 0, 1], # Delays for P4 between rooms
]
# Lunch break time (start of lunch) and duration (in arbitrary time units)
lunch_break = 12 # Lunch break starts at time 5
lunch_duration = 1 # Lunch duration is 1 unit of time
# Create the solver instance and solve the problem
solver = MaintenanceScheduleSolver(rooms, personnel, availability, skills, times, delays, lunch_break, lunch_duration)
solver.solve()Solution: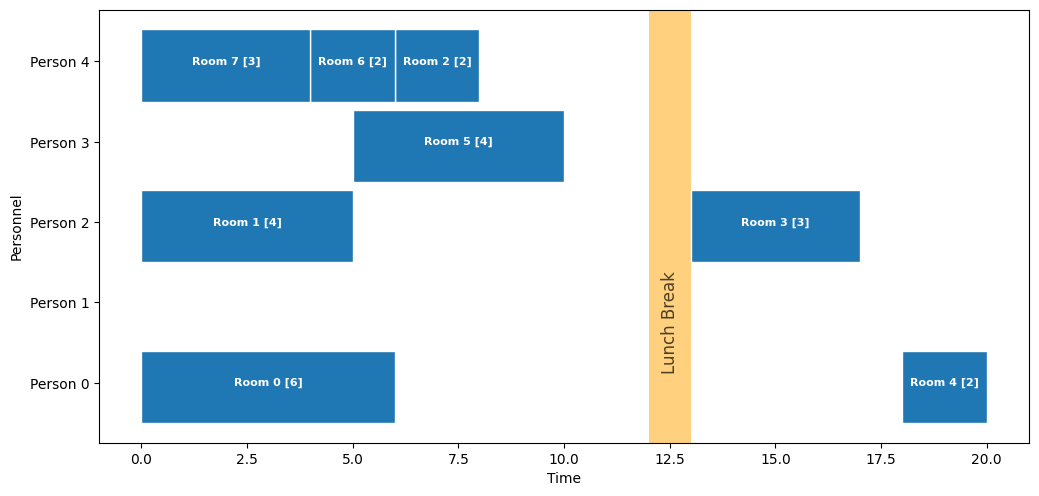
Person 0:
[0, 6]: 0
[18, 20]: 4
Person 1:
Person 2:
[0, 5]: 1
[13, 17]: 3
Person 3:
[5, 10]: 5
Person 4:
[0, 4]: 7
[4, 6]: 6
[6, 8]: 2