Teleportation topology
Quantum Computing, Quantum Field Theory
- I. Introduction
- II. Elements of quantum mechanics
- III. The electromagnetic field
- IV. The qubit
- V. Quantum gates
- VI. States and operators
- VII. Shor’s algorithm
- VIII. Quantum teleportation
- IX. The Deutsch algorithm
- X. The no-cloning theorem
- XI. About anyons
- XII. About SU(2)
- XIII. Teleportation topology
- XIV. The Simon algorithm
- XV. Superdense coding
- XVI. Chern-Simons theory
- XVII. The toric code
- REF. Some pointers
There is race among the technology giants to build a commercial quantum computer or, at least, to achieve mainstream consumption of quantum algorithms on top of some affordable hardware. It’s no secret that Microsoft pushes the frontier via a less common path based on topological considerations. The main reason for taking this approach is because quantum error correction is a big deal if you use other methods (say, based on atomic spin or lasers). A topological quantum computer, on the other hand, is all about knots and braids which are (almost by definition) stable under deformations (homemorphisms).
In this note I only want to highlight how knots enter naturally in the context of teleportation. See an earlier article for an intro and the related articles on quantum computing.
Let’s imagine that Alice and Bob are separated and teleporting a qubit. If we would wish to represent this in a Feynman-like type of diagram it would require an annihilation-creation pair like depicted in the image below.
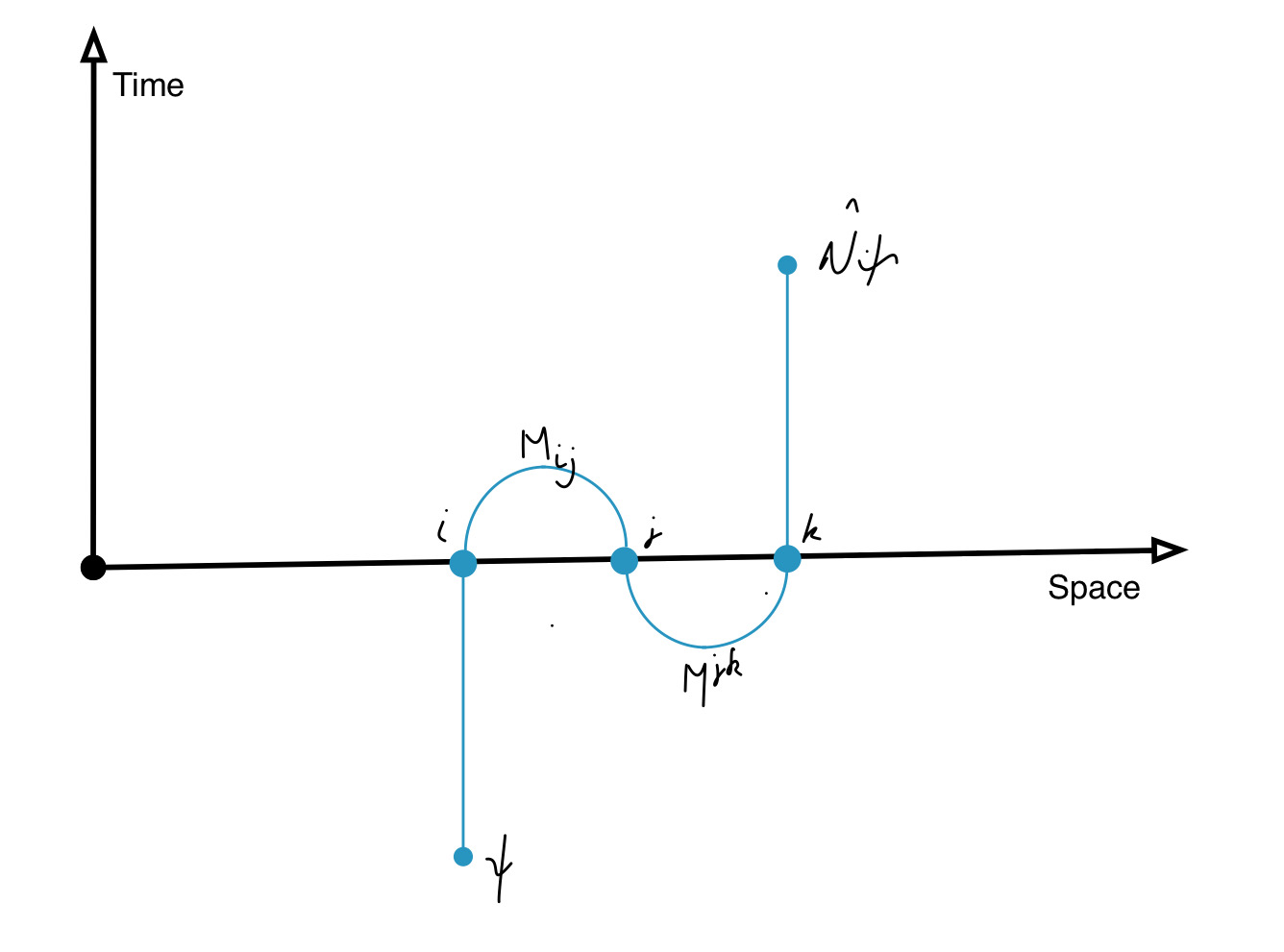
Alice start off with a state \(\left|\psi\right\rangle\) and Bob ends up with a state \(N\,\left|\psi\right\rangle\) with identical characteristics except it’s translated in space and possibly a different phase. The relation between the operators \(N, M\) is easy to see
\[N \left|\psi\right\rangle = M^\dagger.M\left|\psi\right\rangle\\ =\sum M^\dagger {\left|j\right\rangle\left\langle j\right| M} \left|k\right\rangle{\left\langle k\right|}{\,\psi^m\left|m\right\rangle} \\ = \sum \psi^i M^{jk}M_{ki}\left|j\right\rangle \\ = N\left|\psi\right\rangle\]
provided that
\[ N\delta^j_i = \sum M^{jk}M_{ki}\]
and \(N\) is an operator which does not act on the qubit basis but on the spacelike parameter only. This corresponds to the identity operation
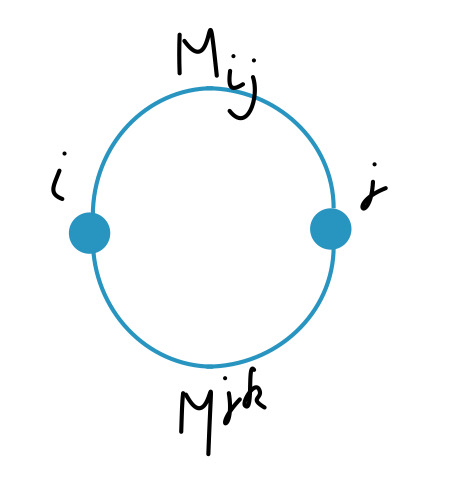
In fact, you can go as wild as you like in representing this:

and as long as you donnot break/interrupt the line you can knot it too

If you agree that the diagrammatic representations are the same you enforce constraints on the operator \(M\). Besides the conceptual idea that all unknots are the same there are also reasons coming from quantum field theory to consider this equivalence. The path-integral representation is directly linked to the idea that a quantum process is probabilistic and all sorts of wild paths are allowed. The same with teleportion, we donnot know what happens between teleportation and all options are allowed.
The constraints on the operator M is related to the Yang-Baxter relations, the Reidemeister moves and braids but this is a chapter on its own. A lesser known fact related to quantum computing is that topological entanglement (knots) and quantum entanglement are intimately related. The operator \(M\) which cannot be written as a tensor product (the very definition of quantum entanglement) implies unknots. The technical translation of this is described in the paper “Yang-Baxter operators need quantum entanglement to distinguish knots” by Alagic et al.
Any solution to the Yang-Baxter equation yields a family of representations of braid groups. Under certain conditions the appropriately normalized trace of these representations yields a link invariant. Any Yang-Baxter solution can be interpreted as a two- qudit quantum gate. If this gate is non-entangling, then the resulting invariant of knots is trivial. One thus obtains a general connection between topological entanglement and quantum entanglement.
A nice technical overview of all this can be found in “A short introduction to topological quantum computing” while a smooth popular version is available (in the Scientific American) under the title “Computing with quantum knots”.
The reason all of this matters is because, as can be seen in the picture above, the whole process is stable under arbitrary shifts and knotting of the process. As such, if one uses braids and links to create a quantum computer the issue of error correcting becomes (in theory) obsolete. This is precisely what topological quantum computers are about and the underlying ‘particles’ are called anyons. Much like phonons, solitons and whatnot, an anyons is a pseudo-particle on top of real matter. The experimental evidence for the so-called non-Abelian anyon is still not very conclusive but is proven theoretically. Given all this, it’s understandable that a company (like Microsoft) has taken this path and if they succeed will harvest the commercial benefits. The race is on.