import networkx as nx
import numpy as np
g = nx.karate_club_graph()
# the adjacency matrix
A = nx.adj_matrix(g)
# the Laplacian
Delta = nx.laplacian_matrix(g)
# from the formula we can get the degree matrix
D = A.toarray() + Delta.toarray()
# to confirm, you can take the degrees explicitly
print(np.diag(D))
print([nx.degree(g, u) for u in g.nodes])Graph Laplacian
The following is a classic setup in physics with springs attached to to gliders. The vertical position is continuous but the horizontal position is fixed. This dynamical system can be described by simple Newtonian mechanics.
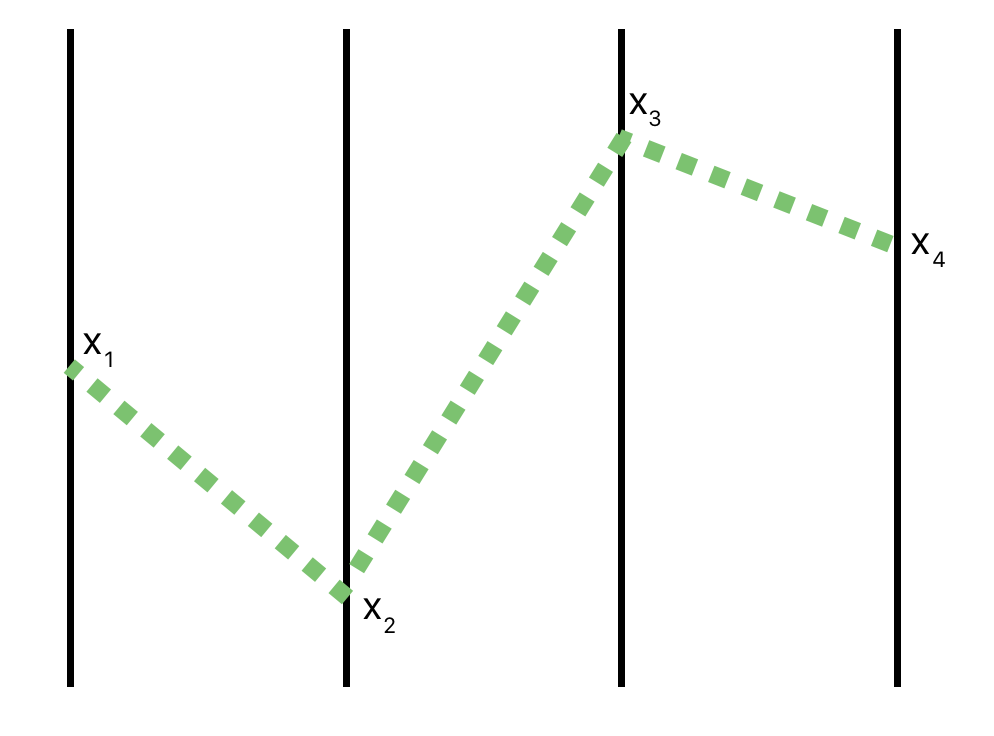
If \(x_i\) is the vertical position of each glider we can form a vector \(\vec{x} = (x_1, x_2\ldots)\) and if every spring has Hooke constant \(k\) the system can be described as:
\[ m\frac{d^2 x_i}{dt^2} = -k (x_i-x_{i+1}) -k(x_i-x_{i-1}) \] If we bring the mass \(m\) to the other side or assume unit mass this can be simplified as:
\[ \frac{d^2 x_i}{dt^2} = -\omega\,(-x_{i-1} +2x_i -x_{i+1}) \] Or equivalently
\[ \frac{d^2 \vec{x}}{dt^2} = \underset{\Delta}{\underbrace{\begin{bmatrix}1&-1&&&&&\\-1&2&-1&&&&\\&-1&2&-1&&&\\&&&\ddots\\&&&-1&2&-1 \\&&&&-1&1\end{bmatrix}}}\vec{x} \] If we define \(D = (d_1, d_2\ldots)\) as the degree and \(A\) the adjacency matrix we get \(\Delta = D - A\) and this is called the Laplacian of the graph. Which graph? Well, the undirected line graph

with adjacency matrix
\[ A = \begin{bmatrix}0&-1&&&&&\\-1&0&-1&&&&\\&-1&0&-1&&&\\&&&\ddots\\&&&-1&0&-1 \\&&&&-1&1\end{bmatrix} \]
Calling the matrix above the Laplacian is based on the similarity of the equation with the continuous case. In classic field theory this would lead to \(\Box\, \phi= (\partial^2/\partial t^2 - \partial^2/\partial x^2)\vec{\phi} = 0.\)
This graph Laplacian is derived on the basis of a line graph but the definition generalizes to arbitrary graphs.
The graph Laplacian can also be obtained by looking at the discrete change of a scalar field on a graph \(f\) (i.e. every vertex \(i\) has value \(f_i\)) and defining
\[ \frac{\partial f}{\partial x_{ij}} = f_j - f_i \] That is, we take the difference in a direction at a vertex provided there is an edge. Summing this gradient in all directions leads to:
\[ \sum_j{\frac{\partial f}{\partial x_{ij}}} = \sum_j f_j -\sum_j f_i = (Df-Af)_i = (\Delta f)_i \] The total derivative at a vertex is the graph Laplacian. This is somewhat difficult to translate to the continuous case since the sum \(\partial/\partial x + \partial/\partial y + \partial/\partial z\) is a first order differential operation while the continuous Laplacian is a second order differential. In this sense, the graph Laplacian measures change and not acceleration.
If we take the definition of the graph Laplacian like this we can write down the diffusion on graphs:
\[ \frac{d\vec{u}}{dt} = -c\, \Delta \vec{u} \] with \(c\) some arbitrary diffusion constant. Let \(\lambda_1, \lambda_2\ldots\) be the eigenvalues of the Laplacian and \(\vec{v}_1, \vec{v}_2\ldots\) the corresponding eigenvectors:
\[ \Delta \vec{v}_i = \lambda_i\,\vec{v}_i \] We can decompose any (time dependent) solution as \(\vec{u}(t) = \sum_i a_i(t) \vec{v}_i\) : \[ \frac{d a_i(t)}{dt} +c\,\lambda_i a_i(t) = 0. \] leading to
\[ a_i(t) = a_i(0) \,e^{ - c\,\lambda_i \, t}. \] This is called the spectral solution of the diffusion equation.
In the spring system above you can see that the sum of each row in the Laplacian is zero. This is general, simply because of the definition of degree and the definition of the adjacency graph. This implies that the Laplacian is singular. Why? The sum of the rows equal to zero can be expressed as \(A.\mathbb{1}=0\) with \(\mathbb{1} = (1,1\ldots)\). This contradicts that there is an inverse which would lead to \(A^{-1}.A.\mathbb{1} = \mathbb{1}=0.\)
Since the Laplacian is singular it necessarily has at least one zero eigenvalue and we can rearrange things to assume that \(\lambda_1 = 0.\) The corresponding eigenvector consists of all 1’s since this is the sum of the rows leading to zeros:
\[ A.\mathbb{1} = \lambda_1\, \mathbb{1} = 0. \] If \(B\) is the incidence matrix of an orientation of \(G\), then \(L=BB^T\). So
\[ x^T\Delta x = \|Bx\|^2 \ge 0\] for all \(x\). The matrix has rows indexed by the vertices, columns by edges and the \(ij\)-entry is 1 if the \(i\)-th vertex is the head of the \(j\)-th edge, \(-1\) if its the tail and 0 otherwise. The eigenvalues are hence all positive. This fits with the expectation that the diffusion equation should, well, diffuse and not explode. Equally well, if there would be a spreading of a disease on a graph the spreading should exponentially decrease over time.
An interesting property of the Laplacian eigenvalues is the following: the number of zeros corresponds to the amount of connected components. See here for a proof, but it’s available in many textbooks as well.
Coming back to the diffusion equation, the initial state \(\vec{u}(0)\) can be used to expressed the coefficients:
\[ a_i(0) = \frac{\vec{u}(0).\vec{v}_j}{\vec{v}_j.\vec{v}_j} \] If we look at the asymptotic solution of the diffusion equation, knowing that all the eigenvalues are positive, we can conclude that
\[ \vec{u}_\infty = a_1(0) \, \vec{v}_1 \] and since the first eigenvector consists of 1’s only:
\[ \vec{u}_\infty = \frac{u_1(0)+\ldots+u_n(0)}{n}\,\mathbb{1} \] meaning that all the nodes in the graph get the average of the initial state. The diffusion leads to equilibrium across the graph. This corresponds to the intuition in the continuous case that a droplet of ink in water diffuses equally across the fluid after a long time.
Note that the asymptotic solution is also the solution to \(\Delta \vec{u}_\infty =0.\)
NetworkX Exploration
The above can be easily explored in NetworkX. Let’s take the classic Karate Club graph
[16 9 10 6 ... 17]
[16 9 10 6 ... 17]The eigenvalues can be obtained via the laplacian_spectrum method:
eigenvalues = nx.laplacian_spectrum(g)
np.round(eigenvalues,2)array([-0. , 0.47, 0.91, 1.13, 1.26, 1.6 , 1.76, 1.83, 1.96,
2. , 2. , 2. , 2. , 2. , 2.49, 2.75, 3.01, 3.24,
3.38, 3.38, 3.47, 4.28, 4.48, 4.58, 5.38, 5.62, 6.33,
6.52, 7. , 9.78, 10.92, 13.31, 17.06, 18.14])You can see that the first eigenvalue is indeed zero and that it has multiplicity one, meaning that the graph is connected. The Karate Club has one (weakly) connected component.
The eigenvectors are not directly available in NetworkX but you can use Scipy for this:
from scipy.linalg import eigh
# Calculate the eigenvalues and eigenvectors of the Laplacian
eigenvalues, eigenvectors = eigh(Delta.toarray())
np.round(eigenvectors, 1)array([[-0.2, -0.1, -0.1, ..., 0.1, 0.9, -0.2],
[-0.2, -0. , -0.1, ..., -0.1, -0.1, -0. ],
[-0.2, 0. , -0. , ..., 0.3, -0.1, -0. ],
...,
[-0.2, 0.1, 0. , ..., 0.1, -0.1, 0.1],
[-0.2, 0.1, 0. , ..., -0.9, 0.1, 0.1],
[-0.2, 0.1, 0. , ..., -0. , -0.2, -0.9]])Note that the first column is the unit (up to an irrelevant scaling factor) corresponding to the zero eigenvalue.