Series parallel Layout
Overview
Series-parallel graphs are a specialized form of directed graphs characterized by having a unique source node, which is the origin point with no edges feeding into it, and a unique sink node, which serves as the termination point with no edges leading out from it. These graphs are constructed through a recursive process that involves two fundamental operations: series composition and parallel composition.
The series composition involves connecting two graphs in sequence, where the sink of the first graph becomes the source of the second. On the other hand, the parallel composition involves connecting two graphs side-by-side, where their respective sources and sinks are merged to form a single source and sink.
The Series-parallel Layout algorithm is designed to visually organize these graphs in a way that accentuates the primary flow direction, which is from the source to the sink. This layout is particularly effective because it simplifies the paths within the graph by minimizing the number of bends in the edges, thereby making the overall structure clearer and easier to follow.
This layout algorithm shares some commonalities with the Hierarchic Layout, but it is generally more efficient in terms of computational speed. However, it’s important to note that the Series-parallel Layout is applicable exclusively to series-parallel graphs due to their specific structure. In contrast, the Hierarchic Layout is more versatile and can be applied to any kind of graph, regardless of its structure.
Series-parallel diagrams, owing to their clear and streamlined representation, are highly suitable for depicting various types of hierarchical structures and processes. They are commonly used in the visualization of electrical circuits, where the flow of current can be traced from the source to the sink. Additionally, they are effective in representing call trees in computer programming, illustrating the sequence of function calls and executions. Flowcharts also benefit from this type of diagram, as they often require a clear demonstration of the step-by-step process or decision-making flow within a system.
Features
The SeriesParallelLayout algorithm is adept at incorporating strong PortConstraints, ensuring that edges are connected to predetermined locations on the nodes. While the specific positions are respected, the directional preferences indicated by the constraints are disregarded.
When it comes to organizing nodes into groups, the SeriesParallelLayout algorithm can effectively manage this task. It is crucial for a group node to encompass an entire series-parallel subgraph to prevent any overlapping with other group nodes or individual nodes. The algorithm prohibits edges from connecting to group nodes that contain other elements. Additionally, users have the option to define minimum size requirements for each group node by utilizing the MINIMUM_NODE_SIZE_DP_KEY provided by the IDataProvider.
The algorithm is configurable to accommodate node labels, ensuring they have reserved space and are not obscured by other elements in the graph. Edge labels are strategically placed along the edges based on the settings in a PreferredPlacementDescriptor. However, labels intended to be centered between the source and target nodes are typically positioned near the target node, except when the edge in question is part of a local subgraph’s source and sink.
For parallel subgraphs, the SeriesParallelLayout algorithm offers various alignment options. The choice of alignment can be influenced by the sizes of the nodes, with certain alignments contributing to a more compact layout.
The distribution of edges around their associated nodes is determined by the ISeriesParallelLayoutPortAssignment instance. The default port assignment takes into account both PortConstraints and edge groups.
The “From Sketch” mode of the algorithm considers the initial positions of the nodes while avoiding the introduction of crossings, thereby preserving the hierarchical order of the nodes’ children.
Custom sorting of a node’s outgoing edges is supported by the SeriesParallelLayout algorithm. This is achieved by assigning an IComparer<T> to nodes individually, which is accessed through an IDataProvider registered with the OUT_EDGE_COMPARER_DP_KEY. In cases where the IDataProvider does not provide a comparator for a node, the algorithm defaults to using a standard comparator.
By default, the SeriesParallelLayout algorithm is tailored for graphs with a series-parallel structure. To adapt it for general graphs, the general graph handling feature must be enabled. This allows the algorithm to modify the input graph by temporarily adding or removing edges to achieve a series-parallel structure. Edges that are removed during this process are routed separately once the main layout is complete. This ensures that the algorithm can be applied to a wider range of graphs while still providing an organized and efficient layout.
Layout
Series-parallel graphs are a specific category of directed graphs that are defined by having exactly one source node, which is characterized by the absence of incoming edges, and one sink node, which has no outgoing edges. The construction of these graphs is governed by two fundamental rules:
Series Composition: This rule involves combining two subgraphs by merging the source node of one subgraph with the sink node of another. This effectively extends the path of the graph, maintaining the directional flow from the original source to the new sink.
Parallel Composition: Under this rule, two subgraphs are joined by merging their respective source nodes into a single source and their sink nodes into a single sink. This creates parallel paths within the graph, allowing for multiple routes from the unified source to the unified sink.
The inherent recursive structure of series-parallel graphs lends itself to the formation of a decomposition tree during the layout process. Each node within this tree symbolizes a specific type of decomposition—either series or parallel. The layout algorithm then proceeds to traverse this tree in a bottom-up fashion. It systematically aligns the subgraphs either vertically (in the case of series composition) or horizontally (for parallel composition), progressively building up the overall structure of the graph until it is fully arranged. Once both end nodes of an edge are positioned, the edge itself is routed. The algorithm can employ various routing styles to optimize the visual clarity and flow of the graph.
To enhance the efficiency of the layout process and minimize the need for relocating nodes multiple times, the algorithm maintains a record of the geometric shapes representing the occupied area of the subtrees. These shapes are dynamically adjusted and combined as the layout calculation progresses. Additionally, the algorithm keeps a record of the connections between nodes, particularly focusing on those nodes that have not yet been positioned within the layout. This ensures that the final arrangement of the graph is both aesthetically pleasing and functionally coherent, with a clear depiction of the flow from the source to the sink and an organized presentation of parallel and series paths.
Business Domains
Electrical Engineering: Within the realm of electrical engineering, series-parallel layouts are pivotal for the design and analysis of electrical circuits. They offer a visual representation of the flow of electrical current and delineate the relationships between various circuit components such as resistors, capacitors, and inductors. By using these layouts, engineers can easily identify series and parallel connections, analyze the impact of each component on the overall circuit, and troubleshoot issues more effectively.
Software Development: In software development, series-parallel layouts are utilized to depict call trees. These trees are visual representations of the sequence of function calls within a program, providing developers with a clear understanding of the program’s execution flow. This is particularly useful for debugging and optimizing code, as it helps in pinpointing performance bottlenecks and understanding the hierarchy of function calls.
Project Management: Project managers often rely on flowcharts designed with series-parallel layouts to map out the sequence of tasks or decisions within a project. These flowcharts serve as a visual tool to identify task dependencies, process steps, and decision points, facilitating better planning and coordination among team members. They also help in predicting potential delays and devising contingency plans.
Manufacturing: In the manufacturing sector, process diagrams that utilize series-parallel layouts are essential for outlining the stages of manufacturing or assembly lines. These diagrams provide a clear view of the sequence of operations and the parallel processes that occur simultaneously. This aids in optimizing the manufacturing flow, reducing downtime, and ensuring that resources are allocated efficiently.
Telecommunications: For telecommunications networks, series-parallel layouts are beneficial in creating network diagrams that clearly illustrate the paths of communication. They highlight points of convergence and divergence within the network, aiding in the design and maintenance of robust communication systems. These layouts are crucial for identifying the most efficient routing paths and for troubleshooting network issues.
Transportation: In the field of logistics and transportation planning, series-parallel diagrams are used to plot out routes and schedules. They emphasize the main arteries of transport, potential bottlenecks, and alternative routes. This helps in optimizing delivery times, reducing transit costs, and improving overall supply chain efficiency.
Technical Details
Playgrounds
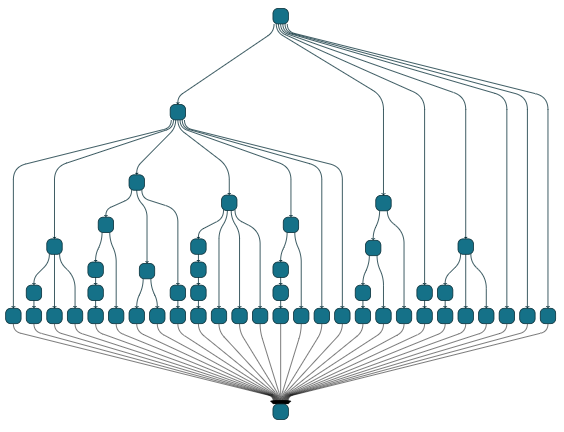
const nodeCount = 50;
const nodes: INode[] = [graph.createNode()]
for (let i = 1; i < nodeCount; i++) {
nodes.push(graph.createNode())
graph.createEdge(nodes[Math.floor(Math.random() * (i - 1))], nodes[i])
}
graphComponent.graph.edgeDefaults.style=new PolylineEdgeStyle(
{
targetArrow:"triangle",
smoothingLength:100
}
)
const setStyle = (u)=> graph.setStyle(u, new ShapeNodeStyle({fill:"red"}));
const a = new YGraphAdapter(graph)
// collect the leafs
const leafs = graph.nodes.filter(u=>graph.outEdgesAt(u).size===0).toArray()
const sink = graph.createNode();
leafs.forEach(u=>{
graph.createEdge(u,sink)
})
const layout = new SeriesParallelLayout({
routingStyle:"polyline",
orientationLayoutEnabled:true,
layoutOrientation:"top-to-bottom",
verticalAlignment:2
});
// layout.appendStage(treeReductionStage);
await graphComponent.morphLayout(layout, '1s')