Compact disc Layout
Overview
The Compact Disk Layout algorithm is a clever strategy for positioning nodes within a circular space, aiming to maximize density while minimizing the disk’s radius. Imagine a virtual disk where nodes are meticulously placed like a well-organized constellation of stars. Here’s how it works:
Node Placement:
- The nodes are distributed across the disk’s surface, ensuring they are as close together as possible.
- The primary objective is to achieve a dense arrangement of nodes, emphasizing their spatial proximity.
Disk Radius Minimization:
- The layout algorithm strives to minimize the radius of the enclosing disk.
- By doing so, it creates a compact representation of the graph, efficiently utilizing the available circular canvas.
Node-Edge Balance:
- While edges (connections between nodes) are considered, they play a secondary role in this layout.
- The focus remains on packing nodes densely, with edges serving as connecting threads.
Ideal Use Cases:
- The compact disk layout shines in scenarios where the graph consists of small components or subgraphs.
- These components may have loosely connected nodes that need to be grouped together and confined within a limited area.
- Think of it as arranging a handful of stars within a cosmic disk—each star representing a node, and the disk representing the canvas.
Group Consideration:
- The algorithm acknowledges the existence of groups within the graph.
- It can accommodate nodes that belong to specific clusters or categories, ensuring they maintain their relative positions.
Edge Challenges:
- However, there’s a caveat: when edges traverse the center of the disk, they can create clutter.
- In graphs with few edges or small components, this issue is less pronounced.
- But as the number of edges increases, the risk of visual chaos grows.
Winding Paths:
- One of the delightful features of the compact disk layout is its suitability for winding paths.
- Imagine a labyrinthine trail spiraling around the center of the disk, connecting nodes in an elegant dance.
- It’s like tracing a celestial path around a cosmic nucleus.
In summary, the compact disk layout is an artful dance of nodes, edges, and circular geometry. It’s perfect for encapsulating small graph components, creating visually pleasing arrangements, and winding paths that lead us deeper into the heart of the graph.
Features
Connected Components
The CompactDiskLayout is a powerful tool that has the ability to take into account the connected components when placing nodes. This is its default behavior. Connected components are groups of nodes that are interconnected. When the CompactDiskLayout is used, it ensures that nodes belonging to the same connected component are placed in a sequential manner during the iterative placement process. This sequential placement of nodes from the same component results in the formation of a visual component. This visual component is a group of nodes that are visually grouped together, making it easier to identify nodes that belong to the same connected component.
Node Types
In addition to connected components, the CompactDiskLayout also has the ability to consider node types. Node types are defined characteristics or categories that nodes can belong to. If node types are defined for the nodes in your graph, the CompactDiskLayout will take these into account instead of the connected components. This means that nodes of the same type will be placed closely together, forming a visual component. This can be particularly useful when you want to visually group nodes of the same type together.
From Sketch
The CompactDiskLayout also offers a feature called “fromSketchMode”. This feature allows the layout to consider the coordinates of the input diagram when arranging the nodes on the disk. This can be particularly useful when you want to maintain the relative positions of the nodes from the input diagram in the final layout.
Node Labeling
Another powerful feature of the CompactDiskLayout is its ability to handle node labeling. The layout allows for integrated node labeling, which means that node labels are placed automatically. This automatic placement ensures that labels do not overlap with other labels or graph elements, making the graph easier to read and understand. There are different policies available for placing node labels, allowing you to choose the one that best suits your needs.
This layout is particularly suitable for graphs with few edges or small components. This is because edges may easily cross the center of the disk, which can result in a cluttered appearance. However, it is especially suitable for creating winding paths around a center, making it a great choice for certain types of graphs.
Layout
The CompactDiskLayout is a layout algorithm that arranges the nodes of a graph on a disk, optimizing the compactness of the placement Here’s a conceptual overview of how it works:
Dense Packing: The CompactDiskLayout arranges the nodes on a disk from the inside out, packing them as densely as possible. The goal is to minimize the disk’s radius. This dense placement of nodes is the primary optimization, while the placement of edges plays a minor role.
Iterative Process: The placement of nodes is done through an iterative process. During this process, the layout avoids overlaps between nodes and label overlaps (if activated).
Connected Components: By default, the CompactDiskLayout takes the connected components of the graph into account for the placement of the nodes. Nodes of the same component are placed sequentially in the iterative placement process, ensuring that they form a visual component.
Node Types: If node types are defined, the CompactDiskLayout takes these into account instead of the connected components. Nodes of the same type are placed closely together, forming a visual component.
From Sketch Mode: The CompactDiskLayout can take the coordinates of the input diagram into account when arranging the nodes on the disk. This is done using the
fromSketchMode.Node Labeling: The CompactDiskLayout allows for integrated node labeling. Node labels are placed automatically without generating overlaps with other labels or graph elements.
Business Domains
Network Visualization:
- Social Networks: Compact disk layouts are suitable for visualizing social networks, where nodes represent individuals or entities, and edges denote connections (friendships, collaborations, etc.). The layout ensures that related nodes are grouped closely together on the disk.
- Organizational Charts: Representing hierarchical structures within organizations, such as reporting relationships, departments, and teams, benefits from compact disk layouts.
Software Dependency Graphs:
- Software Architecture: When analyzing software systems, compact disk layouts help visualize dependencies between modules, libraries, and components. Nodes represent software entities, and edges indicate dependencies (e.g., function calls, library imports).
- Package Managers: Visualizing package dependencies in programming languages (e.g., Python, Java) using compact disk layouts aids developers in understanding how packages rely on each other.
Biological Networks:
- Gene Interaction Networks: Compact disk layouts are useful for representing gene regulatory networks, protein-protein interactions, and metabolic pathways. Nodes correspond to genes or proteins, and edges signify interactions or regulatory effects.
- Ecological Food Webs: In ecology, compact disk layouts help visualize predator-prey relationships, trophic levels, and energy flow within ecosystems.
Infrastructure and System Design:
- Network Topology: Compact disk layouts can depict network topologies, including computer networks, communication systems, and sensor networks. Nodes represent devices (routers, switches, sensors), and edges denote connections.
- Circuit Design: For electronic circuits, compact disk layouts assist in organizing components (transistors, resistors, capacitors) and their interconnections.
Document and Content Management:
- Content Relationships: When managing large document repositories or content databases, compact disk layouts help visualize relationships between documents, articles, or web pages. Nodes represent content items, and edges indicate relatedness (e.g., citations, hyperlinks).
- Tag Networks: Representing tags or keywords associated with content (e.g., blog posts, research papers) benefits from compact disk layouts.
Geospatial Data Visualization:
- Geographical Networks: Compact disk layouts can be applied to visualize geographical networks, such as transportation routes, flight connections, or road networks. Nodes represent locations, and edges signify connections (e.g., flights, roads).
- Spatial Clustering: When analyzing spatial data (e.g., crime incidents, disease outbreaks), compact disk layouts help group related locations together.
Remember that the suitability of compact disk layouts depends on the specific characteristics of the graph, such as the presence of small components, loosely connected nodes, and the need for dense placement. These layouts provide a visually compact representation while minimizing edge routing.
Technical Details
Playgrounds
▸ compact disc layout of a long chain
This snippet demonstrates how to use the compact disc layout with a chain graph.

graph.nodeDefaults.style=new ShapeNodeStyle({
shape:"ellipse"
})
const nodeCount = 1500
const rootNode = graph.createNode()
const nodes: INode[] = [rootNode]
for (let i = 1; i < nodeCount; i++) {
const n = graph.createNode();
const r = Math.random()*50;
graph.setNodeLayout(n, new Rect(0,0,r,r));
nodes.push(n)
graph.createEdge(nodes[i-1], nodes[i])
}
const layout = new CompactDiskLayout();
await graphComponent.morphLayout(layout, '2s')▸ compact disk layout with node types grouping
Grouping nodes on the basis of some type is shown in this example where nodes of the same color are taken together in the compact disc layout.
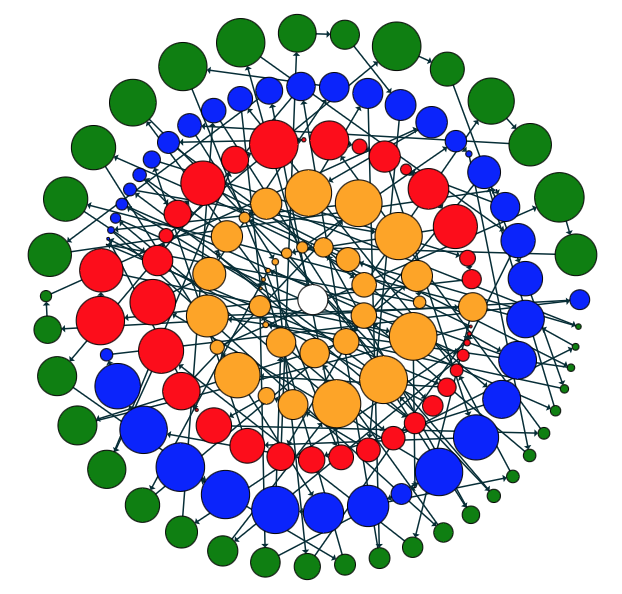
graph.nodeDefaults.style=new ShapeNodeStyle({
shape:"ellipse"
})
const nodeCount = 150
const rootNode = graph.createNode()
rootNode.tag = {group:1}
const nodes: INode[] = [rootNode]
const gids = ["red","orange","green","blue"];
for (let i = 1; i < nodeCount; i++) {
const n = graph.createNode({
tag:{
group: gids[Math.floor(Math.random() * gids.length)]
}
});
const r = Math.random()*50;
graph.setNodeLayout(n, new Rect(0,0,r,r));
graph.setStyle(n, new ShapeNodeStyle({fill:n.tag.group, shape:"ellipse"}))
nodes.push(n)
graph.createEdge(nodes[i-1], nodes[i])
}
const layout = new CompactDiskLayout({ minimumNodeDistance: 4});
const compactDiskData = new CompactDiskLayoutData()
// the node types are taken from an optional nodeType property on the node's tag
compactDiskData.nodeTypes.delegate = (node) => node.tag.group;
await graphComponent.morphLayout(layout, '2s', compactDiskData)