The first 1000 primes with modulo edges can be assembled like so:

The standard base-2 graph looks like the following:

The base-n graphs for n=2,..,100

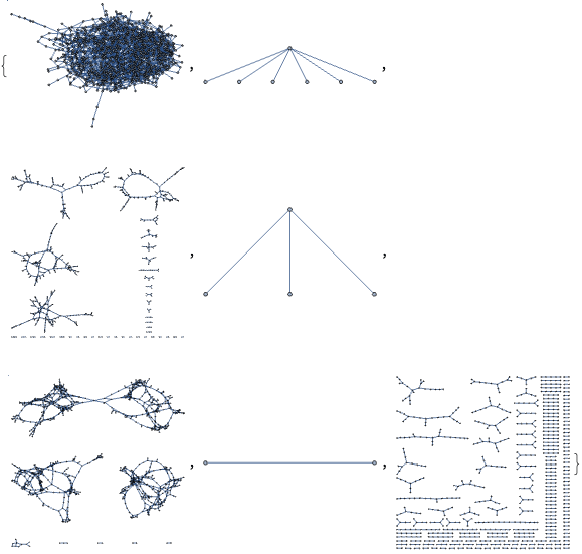
It seems the odd values gives a connected graph except for N=2:

The diameter is obviously ∞ for odd values:

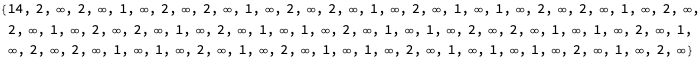
If we take the odd ones only and skip the N=2 exception:

Let’s create an association for this:

Can something be learned here?

Let’s create a test set:

That’s not encouraging. The classifier actually is a simple block function as can be seen from

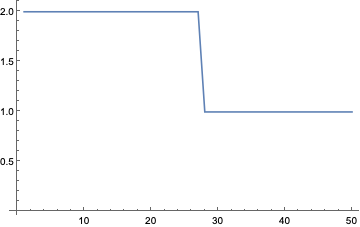
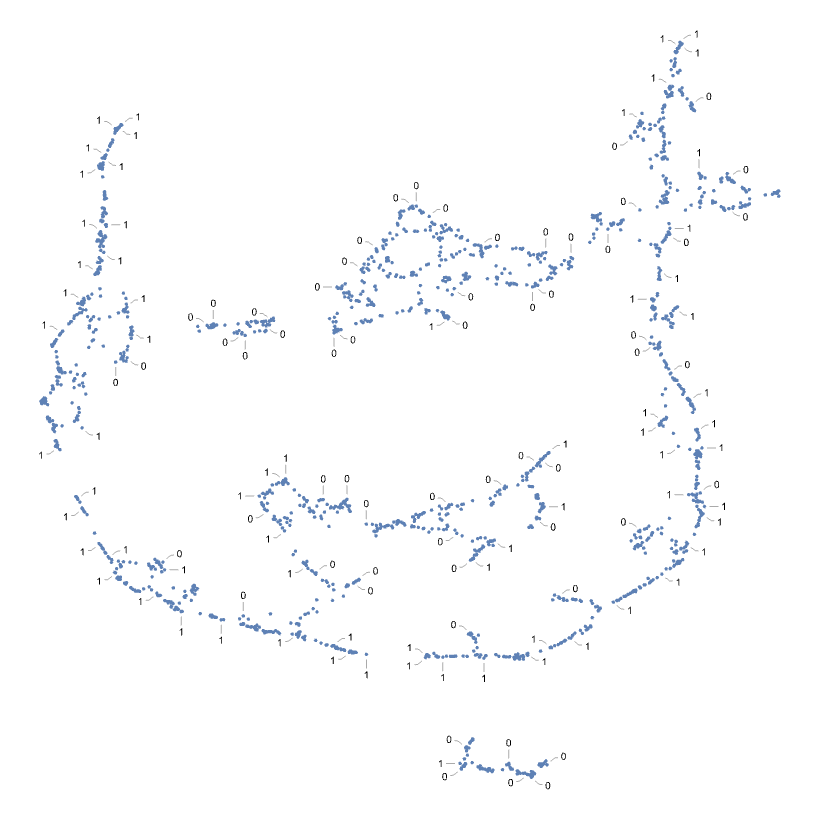
How does it look visually?

Prime base

What about using prime bases? The first 100 primes:

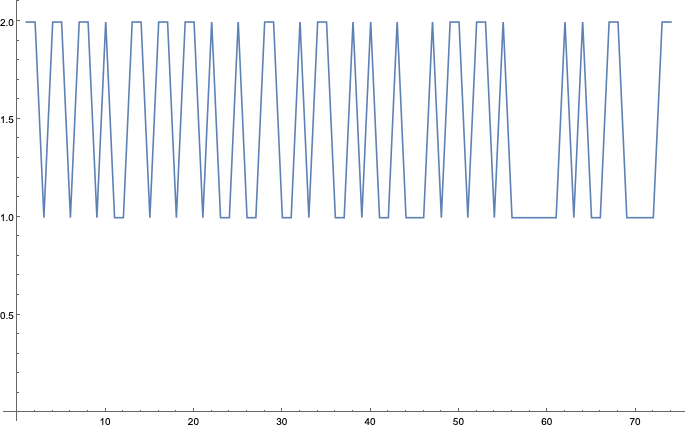
Here again, only N=2 stands out:

More visually:

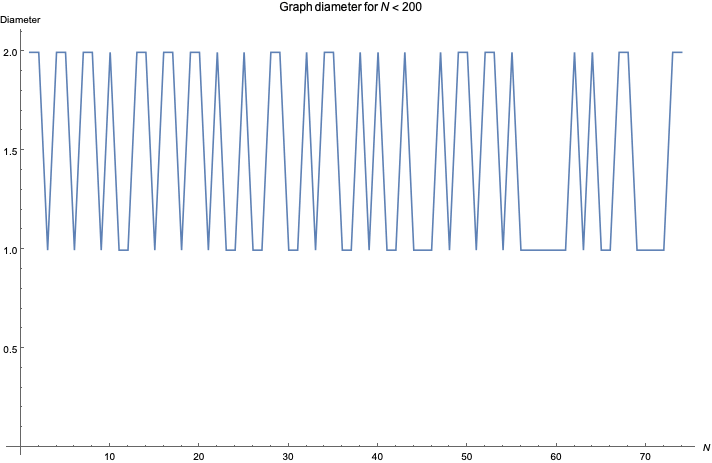
This is equivalent to looking at the graph diameter:

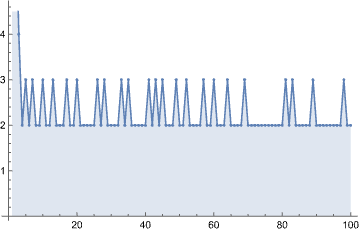
Since it looks so binary, let’s omit the first anomaly and see what number this produces:

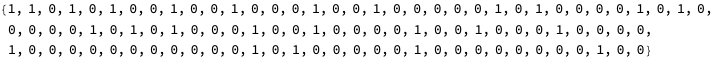
Link prediction

There seems have be some convergence and bands or levels:

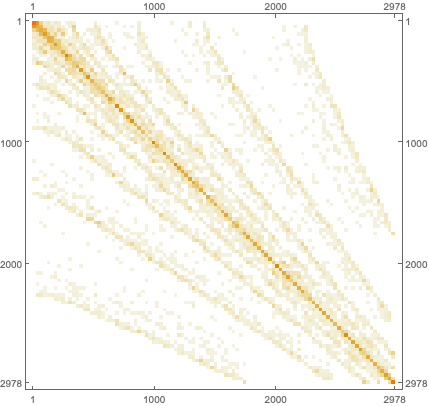
Because of the sparseness we sample in the first 100 primes:

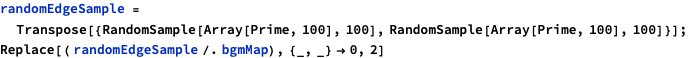
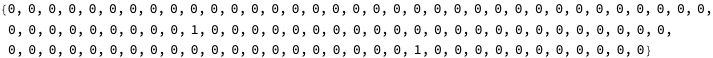
Even all of this leads to a highly imbalanced set to train.

So, have to approach it differently. Let’s take a positive set:

and a negative set:

Let’s combine this into a function:

Now we can generate arbitrary datasets for training and testing:
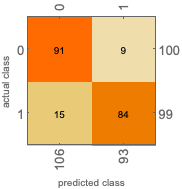